| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- string
- QueryDSL
- git
- JUnit
- Action
- 사이드 프로젝트
- workflow
- mutable
- Spring
- redis
- kotlin
- rds
- immutable
- compiler
- java
- aws
- Github
- 알고리즘
- db
- CodeDeploy
- AOP
- JPA
- springboot
- EC2
- build_test
- 토비의 스프링
- template
- Airflow
- Today
- Total
개발 일기
프로그래머스 레벨2 124 나라의 숫자 (JAVA) 본문

어쩌다 삘이와서 이번에도 레벨2 문제를 풀었다
https://programmers.co.kr/learn/courses/30/lessons/12899
코딩테스트 연습 - 124 나라의 숫자
programmers.co.kr
124 나라의 숫자!
문제는 이러하다
이 나라의 숫자는 모두 1 2 4 로만 표현된다
이진법처럼 말이다
예를 들면
1 -> 1
2 -> 2
3 -> 4
4 -> 11
이렇게 진행된다.
이 문제는 규칙을 나름 생각해서 풀어본 건데
풀리긴 했다.. 이것보다 더 좋은 방법은
무수히 많을 수 있다...
내가 생각한 규칙은 이러하다
n 이 3의 배수일 경우 4를 넣어준 후
n을 3으로 나누고 -1을 뺀 수만큼 다시 또 돌린다..
왜냐면 n의 배수에는 모두 4가 들어가기 때문이다..
어쩌다 보니 규칙을 찾아서 푼 건데 설명하기가 너무 힘든 거 같다..
코드를 보자
이번에는 재귀로 풀었는데
재귀에 대해 참고할만한 블로그를 링크를 걸어두겠다..
https://mijeong611.tistory.com/35
[ 자바 ] 재귀함수란?
[ 자바 ] 재귀함수란? 메서드내부에서 자신의 메서드를 호출하는것 재귀함수의 동작 과정 보통 많이 잘못생각하는 부분이 ( 나도 그랬었고 ) 메서드가 호출될경우 현재 메서드가 실행이 완료되
mijeong611.tistory.com
지인의 블로그인데 재귀에 대해 정리가 되어있다.
모든 코드는 GitHub 에 올려놓았다.
문제에 대한 코드를 보자
class Solution {
StringBuilder builder = new StringBuilder();
public String solution(int n) {
if(n == 0) {
return builder.toString();
}
if(n == 3) {
builder.insert(0, 4);
return builder.toString();
}
if(n < 3) {
builder.insert(0, n);
return builder.toString();
}
if(n % 3 == 0) {
builder.insert(0, 4);
return solution(n / 3 - 1);
} else {
int num = n % 3;
builder.insert(0,num);
n = n / 3;
return solution(n);
}
}
}
/*
1 -> 1
2 -> 2
3 -> 4
4 -> 11 -> 1 1 -> 11
5 -> 12 -> 1 2 -> 12
6 -> 14 -> 2 ->
7 -> 21 -> 2 1 -> 21
8 -> 22 -> 2 2 -> 22
9 -> 24 -> 3
10 -> 41 -> 3 1 -> 41
11 -> 42 -> 3 2 -> 42
12 -> 44 -> 4
13 -> 111 -> 4 1 -> 1 1 1 -> 1 1 1
14 -> 112 -> 4 2 -> 3 1 2 -> 1 1 2
15 -> 114 -> 5
16 -> 121 -> 5 1 -> 3 2 1 ->1 2 1
17 -> 122
18 -> 124
19 -> 141
20 -> 142
21 -> 144
22 -> 211 -> 7 1 -> 2 1 1 -> 211
23 -> 212
24 -> 214
25 -> 221
26 -> 222
27 -> 224
28 -> 241
*/
예시들을 몇 개 둔 건데
n을 3으로 나누고 나머지를 넣어준 후
n / 3으로 나눈 후 다시 공식을 대입한다
11을 예로 들어보자
11은 일단 3으로 안 나눠진다.
그렇다면 11을 3으로 나누면 나머지는 2다 2를 넣어준다
그리고 11을 3으로 나누면 몫은 3이다
한 번 더 공식을 돌리면
3은 4가 된다 4를 넣어주면 42가 나온다..
정리... ( 나도 잘 모르겠다..)
n % 3 == 0 -> 4
(n / 3) - 1
n % 3 != 0 -> n % 3
n / 3
반복
후기
풀긴 풀었는데 남한테 설명하기는 아직 부족한 거 같다.. 노력해야겠다 ㅠㅠ
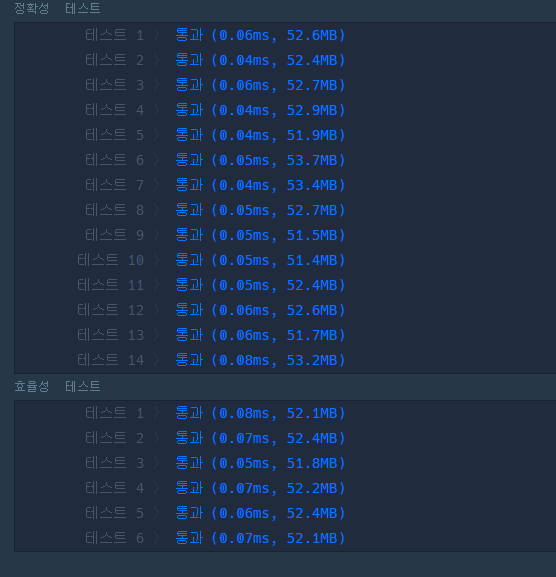
그래도 다른사람들 보면 효율성에서 막혔다는데 나는 효율은 좋았다..!
'알고리즘 > programmers' 카테고리의 다른 글
| 프로그래머스 레벨2 숫자의 표현 (JAVA) (0) | 2021.07.16 |
|---|---|
| 프로그래머스 레벨2 더 맵게 (JAVA) (0) | 2021.07.14 |
| 프로그래머스 레벨2 전화번호 목록 (JAVA) (0) | 2021.07.11 |
| 프로그래머스 레벨2 튜플 (JAVA) (0) | 2021.07.11 |
| 프로그래머스 레벨 2 짝지어 제거하기 (JAVA) (0) | 2021.07.10 |




